About approaches to studying of the microevolutionary phenomena in connatural chironomids populations. nonequilibrium of populations as stable state
- Authors: Zhirov S.V.1, Mylnikov S.V.2
-
Affiliations:
- Zoological Institute
- St Petersburg State University
- Issue: Vol 14, No 3 (2016)
- Pages: 35-46
- Section: Articles
- Submitted: 14.11.2016
- Published: 15.09.2016
- URL: https://journals.eco-vector.com/ecolgenet/article/view/5481
- DOI: https://doi.org/10.17816/ecogen14335-46
- ID: 5481
Cite item
Full Text
Abstract
Keywords
Full Text
ВВЕДЕНИЕ
Количество научных работ, посвященных полиморфизму популяций, поистине необъятно. Независимо от направления (адаптационное или эволюционное), методики получения результатов (генетический анализ, электрофорез, хроматография или прямые хромосомные наблюдения), закономерности популяционной генетики, основанные на законах Менделя, хромосомной теории наследственности, комплементарности нитей ДНК, механизмах мейоза, теории вероятностей, неизменны для систем любой сложности. Математический аппарат, описывающий полиморфизм в панмиктической популяции, хорошо разработан [20, 21, 31]. Однако детерминированные модели всего лишь диплоидной двухлокусной диаллельной популяции уже настолько сложны, что почти неприменимы на практике и имеют, пожалуй, сугубо теоретическое значение [35]. Анализ сложных систем с многочисленными внутренними взаимосвязями неизбежно приводит к росту числа всевозможных допущений в геометрической прогрессии. А дополнительное усложнение математического аппарата, учитывающего эти нюансы, не приближает исследователя к истине, а все дальше уводит в дебри дополнительных условий и ограничений.
Анализ моногенного наследования в случае диаллельного локуса с неполным доминированием у диплоидных организмов — простейшая операция в вычислительном аппарате популяционной генетики, подобно эвклидовой геометрии или ньютоновской физике в общей картине современной науки. Однако, несмотря на эту обманчивую простоту, она является краеугольным камнем популяционного анализа. В основе положения о равновесности популяций лежит закон Харди – Вайнберга, который эксплицируется биномиальным распределением, его простейшим случаем является формула Пирсона.
p2 + 2pq + q2 = 1,
где p — частота доминантного, а q — рецессивного аллеля. Этой же формулой описывается кодоминирование. Важно, что генотипы с частотами p2, 2pq и q2 различимы в данном поколении визуально или с помощью лабораторных методов, но без дополнительных скрещиваний, то есть без генетического анализа. Эти три класса генотипов в отечественной литературе обозначаются как P, H и Q [32].
Вышеприведенная формула Пирсона — наиболее простая математическая модель, и поэтому она обременена множеством условностей.
1. Популяция изолирована (нет миграции, либо эмиграция и иммиграция уравновешивают друг друга).
2. Аллели не возникают заново (нет мутаций), популяция достаточно большая (нет дрейфа генов, эффект основателя не проявляется).
3. Вероятность скрещивания конкретных генотипов пропорциональна частотам этих генотипов в популяции.
4. Особи имеют равную жизнеспособность и выживаемость от зиготы до репродуктивного возраста.
5. Исследуемые аллели не сцеплены с полом.
6. Исследуемые аллели локализованы в ядерных генах.
Эти условия характеризуют так называемую «элементарную популяцию» — основную эволюционную единицу.
Удобными объектами для изучения популяционных явлений в естественных условиях среды служат организмы с небольшим числом хромосом, например насекомые из отряда двукрылых. Роль плодовой мушки из рода Drosophila в становлении, в частности, популяционной генетики трудно переоценить. Немаловажное место в генетических исследованиях занимают также комары-звонцы (Chironomidae), которые характеризуются в среднем относительно малым диплоидным числом хромосом (6–8). Преимуществом этой группы также является несложная видовая идентификация благодаря кариосистематическим исследованиям политенных хромосом (ПХ) из слюнных желез, которые имеют уникальную для каждого вида последовательность дисков и междисков. Ввиду конъюгации гомологов ПХ в интерфазных клетках слюнных желез изучение хромосомных перестроек на основе нарушения последовательности дисков хромосом (ПДХ) не представляет труда. Однако, строго говоря, ПДХ следует рассматривать не как аллели в классическом смысле теории гена, а как альтернативные группы сцепления, ведущие себя как классические аллели в процессе наследования. Не раз поднимался вопрос о том, что ПДХ на самом деле являются фенами и модели, основанные на анализе политенных хромосом, при котором возможно отчетливое визуальное разделение генотипов, должны подчиняться закономерностям фенетики. По нашему мнению, противоречия нет. Разница лишь в том, что фенетика изучает непрерывное распределение признаков. И при сокращении числа фенов (при моногибридном скрещивании до трех) распределение становится дискретным и доступно для популяционного анализа на предмет проверки соответствия формуле Пирсона. Таким образом, ПХ являются уникальным объектом, находящимся на границе генетики и фенетики.
Изучая популяционные явления у таких организмов, как хирономиды, далеко не всегда можно провести полноценный мониторинг вследствие того, что их местообитания нередко эфемерны (пересыхающие, промерзающие, меняющие русло и антропогенно уязвимые), а взрослые особи в период размножения активно или пассивно могут преодолевать значительные расстояния от точки вылета и оставлять кладки уже в других водоемах. Поэтому нередко приходится довольствоваться данными скрининга, полученными в результате анализа только одного поколения.
При исследованиях хромосомного полиморфизма у хирономид принято оценивать такие величины, как средняя гетерозиготность по хромосомным инверсиям, частоты генотипов с гетерозиготами [3, 17]. Учитывают также зиготические сочетания (ЗС) перестроек в кариотипе (что имеет смысл при достаточно больших выборках) и их спектр в популяции [18]. Значительно реже приводят дифференцированную информацию о соотношении гомозигот, гетерозигот и гомозигот по инверсиям. Нередко реальные частоты этих ЗС в природных популяциях далеки от ожидаемых частот по формуле Пирсона.
Считается, что анализ одного поколения не способен выявить динамические процессы, происходящие в популяции, и факторы, стабилизирующие или нарушающие ее равновесие [15, 32]. Можно поспорить с категоричностью этого утверждения. Изменение подхода к анализу фактических данных может помочь спрогнозировать порядок искомых величин даже в случае единичного временного среза. Наиболее наглядно это можно продемонстрировать на вышеописанной модели. Чтобы иметь возможность проанализировать приспособленность и степень давления отбора в данной модели, необходимо еще одно допущение — что отбор действует только против одного класса из трех. Математически это можно выразить следующим образом: p2 + 2pq + (q2 + X) = 1, где X — частота гомозиготных по рецессивному аллелю особей, утерянных вследствие элиминации. Имеем квадратное уравнение с одним неизвестным, которое легко решить по формуле или системой уравнений. Если же давлению отбора подвергаются остальные классы, анализ теряет смысл, поскольку в формуле появляются дополнительные независимые неизвестные: (p2 + Z) + + (2pq + Y) + (q2 + X) = 1, где X, Y и Z — частоты вымерших особей в каждом классе. Эти переменные только частично взаимозависимы: чтобы вычислить одно из трех неизвестных, нужно знать значения двух других. Уравнение Пирсона с двумя и тремя неизвестными будет иметь бесконечное число решений или, точнее, ни одного строгого решения.
Данная работа является результатом исследования разовых сборов в популяциях хирономид. Фактически мы описываем методику выполнения популяционного экспресс-теста как альтернативу долговременного мониторинга. Проанализированы возможные направления микроэволюционных процессов на основе скрининга (временного среза).
МАТЕРИАЛ И МЕТОДИКА
Объектом исследования послужили популяции трех высокополиморфных по хромосомным перестройкам видов хирономид из трех разных родов — Chironomus annularius, Camptochironomus tentans и Glyptotendipes glaucus. Эти виды массовые, предпочитают эвтрофные местообитания, как правило, доминируют в хирономидных сообществах и характеризуются трансконтинентальными ареалами. Для анализа отбирали популяции, в кариофонде которых были встречены массовые перестройки, но не более одного типа инверсий для каждого хромосомного плеча, и которые были представлены в сборах достаточно представительными выборками. Личинки хирономид собирали с грунта драгой или скребком, промывали через энтомологические сита. После чего фиксировали на месте в жидкости Кларка (ледяная уксусная кислота и 96 % этиловый спирт 1 : 3). Через час фиксатор заменяли свежим. Фиксированный материал хранили в холодильнике при температуре 4–6 °C. Давленые препараты политенных хромосом из слюнных желез готовили по рутинной методике с модификациями [34]. Сравнение дисковых последовательностей проводили по цитофотокартам и кадастрам ПДХ у данных видов [4, 18, 41]. Фиксировали гетеро- и гомозиготные перестройки. Применяли краткое описание последовательностей без указания точек разрывов (A1, A2 и т. д.).
Сборы C. annularius проводили в 2010 г. в двух местообитаниях в Армении: 1) с. Ранчпар (Араратский р-н, в 25 км от г. Ереван), в стоячем водоеме (84 особи) и 2) в оросительном канале неподалеку от этого же села (94 особи) (сбор М. Арутюновой и К. Арутюновой). C. tentans (40 особей) был собран в 1998 г. в России, Псковская область, г. Псков, р-н Любятово, заболоченный участок р. Ремонтки (сбор С.В. Жирова и Е.Н. Матвеевой). Популяции G. glaucus проанализированы из трех местообитаний: 1) Ленинградская обл., пруд в пос. Усть-Ижора (1993 г.) (29 особей); 2) Тверская обл., оз. Глубокое (1982 г.) (59 особей); 3). Украина, г. Чернобыль, водоем в районе Рыжего леса (1987 г.) (23 особи). (Все сборы сделаны Н. А. Петровой.) По этому виду данные частично опубликованы ранее [24]. В приводимых таблицах местообитания соответственно пронумерованы.
После подсчета частот различных ЗС рассчитывали теоретические соотношения генотипов для данных популяций. При этом использовались два принципиально разных подхода. В первом случае на основе реального количества разных генотипов традиционно подсчитывали наблюдаемые частоты фенов-аллелей и, исходя из них, вычисляли ожидаемые частоты генотипов. Второй подход был основан на предположении, что возможные отклонения от значений в формуле Пирсона были связаны с давлением отбора и элиминацией части потомков. Мы посчитали целесообразным применить метод, когда ожидаемое вычисляется с учетом элиминировавших особей. Было решено сначала «компенсировать» потери наиболее малочисленного класса при отборе и на этой основе оценивать ожидаемое соотношение. Формулы для компенсации опубликованы в методической литературе [5]. Однако применяемые в последнем источнике обозначения частот генотипов как P, Q и R мы посчитали неудачными, так как одной буквой обозначены частоты гетерозигот и частоты рецессивного аллеля (Q и q) и их легко спутать. В итоге мы использовали систему обозначений из работы Н.Н. Хромова-Борисова [32].
Если обозначить частоты генотипов как P, H, Q, то есть P ≡ p2, H ≡ 2pq, Q ≡ q2, тогда:
1) ожидаемое число гетерозигот рассчитывается как H = √ 4PQ = 2√ PQ;
2) недостающие гомозиготы Q вычисляются как Q = (H / 2√ P)2 = H2 / 4P (формула, естественно, подходит и для расчета значения P).
Для «компенсации» выбирали два наибольших значения из тройки генотипов и подставляли их в формулу. Результат округляли до десятых долей. Иногда подход через «наибольшие значения» приводил к тому, что ожидаемое оказывалось еще меньше наблюдаемого. Тогда приходилось использовать наибольшее и наименьшее значения из тройки и снова делать перерасчет.
Далее сравнивали наблюдаемые группы значений с ожидаемыми, используя метод хи-квадрат [26, 28]. Сравнивали попарно: наблюдаемое — ожидаемое классическое и наблюдаемое — ожидаемое «компенсированное». Также рассчитывали индекс фиксации Фишера [39].
Все рассматриваемые случаи представляли собой моногибридное диаллельное скрещивание с неполным доминированием или кодоминированием. На определении порогового значения критерия χ2 стоит остановиться подробнее. Несмотря на то что случай является одним из простейших в исследованиях по генетике, в методической литературе нет согласия о способах определения числа степеней свободы для этого варианта. Методические рекомендации по биологической статистике обычно предлагают упрощенную формулу «число различимых классов (фенотипов) минус 1», то есть 2 [10, 22]. В то же время в большинстве современных работ, посвященных исследованиям полиморфизма белков, используют принцип «число генотипов минус число аллелей», то есть для нашего случая 1 [21, 28, 30, 31]. Ивантер и Коросов допускают разные способы вычисления степеней свободы. Так, например, в случае сравнения моногибридного скрещивания при кодоминировании с биномиальным распределением число степеней свободы равно 0 (число классов минус три параметра: объем выборки, средняя и дисперсия) [14]. И анализ, естественно, становится невозможен. Плохинский в своем классическом труде допускает, что число степеней свободы может составлять как 0, так и 1 в зависимости от условий формулирования гипотезы [26]. Кроме того, когда частоты вероятностей образования разных классов начинают сильно различаться, или в случае малого числа классов биномиальная кривая становится асимметричной и аппроксимируется распределением Пуассона, для которого число степеней свободы в нашем случае равно 1 (число классов минус два параметра: объем выборки и среднее) [19].
Известно, что Пирсон и Фишер вели спор о числе степеней свободы в случае применения критерия χ2 для четырехпольной таблицы. Пирсон рассчитывал эту величину как 4–1 = 3. Фишер утверждал, что уровень значимости критерия при трех степенях свободы излишне мал, а при 1 наиболее точен. В итоге Ньюман и Пирсон совместно провели строгую математическую проверку и показали, что позиция Фишера оказалась верной [8].
В наши дни неоднократно было показано, что в случае попарных сравнений по таблицам сопряженности 2 × 2 величина χ2 только в 5 % случаев превышает величину 3,84, это и есть пороговое значение, которое в справочных таблицах для критерия χ2 соответствует одной степени свободы [9]. Этой точки зрения мы и решили придерживаться.
Итак, при одной степени свободы на уровне значимости p < 0,05 значение критерия равно 3,84, а при p < 0,01 — соответственно 6,63. К сожалению, современные статистические программы рассчитывают значение критерия χ2 по многопольным таблицам без поправки Йетса, которую рекомендуется вводить, когда частота хотя бы одного класса меньше четырех. Однако на общую картину это, как правило, не влияет, и тенденция вполне очевидна. При выполнении статистических расчетов и рисования графиков использовали программу Statistika 10.0.
Для популяции C. tentans, как наиболее полиморфной, проводили сравнение наблюдаемых частот ЗС по числу генотипов и числу особей с ожидаемым для гексагибридного скрещивания, а также с биномиальным.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Chironomus annularius — один из самых широко распространенных видов в роде, в настоящее время кариологически он хорошо изучен. 2n = 8. Цитокомплекс thummi (комбинация хромосомных плеч AB, CD, EF, G). Последовательности дисков, принятые за стандарт, обозначаются цифрой 1 (A1, B1 и т. д.), отличные от стандарта — арабскими цифрами от 2 и далее в порядке хронологии их открытия и изучения. У C. annularius перестройки были обнаружены в пяти плечах из семи: A2, B2, D2, E2, F2. Эти ПДХ являются обычными для Палеарктики [41]. Поскольку выборка достаточно большая, анализировались все типы ЗС. Результаты приведены в таблице 1.
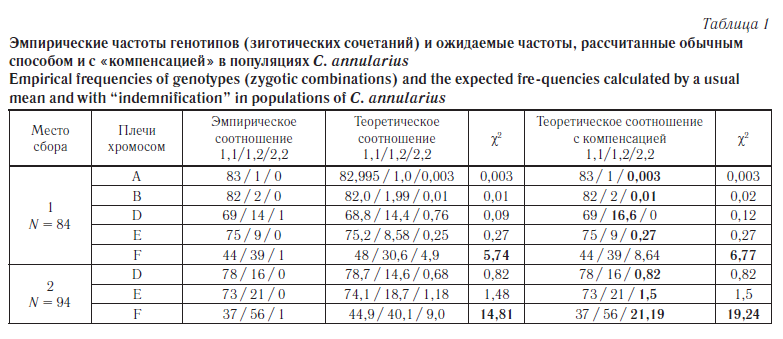
Для C. annularius теоретические и реальные частоты достоверно различались только для плеча F из популяции оросительного канала (χ2=14,81 и χ2 = 19,24), в том числе на уровне значимости p< 0,01. При относительно большой частоте гетерозигот частота гомозигот по инверсиям была необычно мала. В стоячем водоеме для плеча F наблюдался похожий дисбаланс — значение критерия достоверно превышало табличное (χ2 = 5,74). При сравнении наблюдаемой частоты с «компенсированным ожидаемым» различия при заданных условиях также оказались достоверными (χ2 = 6,77). Для остальных плеч эти величины различаются незначительно.
Camptochironomus не так давно был выделен в самостоятельный род. По сравнению с родом Chironomus кариологически он представляет собой другой цитокомплекс, образовавшийся в результате робертсоновской транслокации, с сочетанием хромосомных плеч AB, CF, ED, G. У C. tentans (2n = 8) перестройки обнаружены в шести плечах из семи: A2, B2, C2, F2, D2, G2, они являются обычными для палеарктических популяций [16]. В популяциях C. tentans при подсчете ожидаемых частот «с компенсацией» для плеч А и С рассчитывали значение не для наименьшего значения (гомозигот по инверсиям), а для гетерозигот. Для плеча В «компенсировали» стандартные гомозиготы. Результаты приведены в таблице 2.

В этом случае наблюдается заметная неравновесность по частоте вариантов в плече А, связанная с нехваткой гетерозигот в отличие от ожидаемого значения. Причем различия достоверны при обоих методах расчета, значения критерия χ2 соответственно равны 12,56 и 15,85, в том числе на уровне значимости p < 0,01. Кроме того, судя по частоте перестроек в плече В, наблюдается нехватка гомозигот по «стандартным» последовательностям. Это явление выходит на достоверный уровень p < 0,05 при сравнении с «компенсированными» частотами (χ2 = 7,2), а классический метод позволяет лишь предполагать тенденцию. Такая же тенденция прослеживается в плече G, но достоверно это утверждать нельзя.
Glyptotendipes — род, чьи филетические связи с родом Chironomus на основе дискового рисунка ПХ до сих пор не выявлены. Однако система обозначения плеч хромосом и дисковых последовательностей применяется аналогичная. Для G. glaucus (2n = 8, сочетание плеч AB, CD, EF, G) проводили частотный анализ обычных для Палеарктики последовательностей A2 и B3 [4], так как в остальных хромосомных плечах частота перестроек приближалась к нулю. Поскольку две выборки были относительно невелики, единичные инверсии в остальных плечах мы не учитывали. Для G. glaucus во всех трех популяциях в случае перестроек плеча А рассчитывали компенсацию для гетерозигот. Результаты приведены в таблице 3.

Неравновесность имеет место во всех трех популяциях G. glaucus. Оба метода привели к выводу о достоверных различиях для частот перестроек в плече А. Значения критерия χ2 значительно превышают пограничное, в том числе на уровне значимости p < 0,01. И только в одном случае для плеча В в усть-ижорской популяции «компенсационный» метод показал достоверную нехватку гомозигот по инвертированным последовательностям (9,0). Классический метод эту закономерность также обнаружил на достоверном уровне (p < 0,05), хоть величина критерия и оказалась вдвое меньше (4,46). Таким образом, в популяции G. glaucus, как и в популяции C. annularius, неравновесность также связана с перестройками в плече А. Стоит упомянуть, что чернобыльская популяция по перестройкам в I хромосоме фактически не отличалась от остальных.
Процессы, происходящие практически во всех плечах кариотипа C. annularius, в плечах F, D и G у C. tentans и плече B у G. glaucus — классические примеры того, как рецессивный аллель сохраняется в генофонде благодаря гетерозиготам, которые мы в нашей модели полагаем считать равными по приспособленности гомозиготам по стандартным последовательностям. Следует отметить еще одно редкое явление, когда в популяции C. tentans наблюдается нехватка стандартных последовательностей в гомозиготном состоянии в плече IB. Помимо давления отбора это может иметь и дополнительное объяснение. За стандарт у данного вида была принята ПДХ из западноевропейских популяций, в которых эта ПДХ встречалась наиболее часто. В то время как популяция из Псковской области по генетической структуре гораздо более «восточная».
Можно заметить, что, когда один класс гомозигот отсутствует, компенсирующая величина равна значению хи-квадрат, то есть одновременно является мерой различия выборок. Это обстоятельство может послужить основой для разработки экспресс-теста популяционной структуры, не требующего сложных расчетов.
Неравновесность отмечается, как правило, в тех случаях, когда наблюдается избыток или недостаток гетерозигот. Такие классы заметны визуально, даже без анализа достоверности отличий от теоретически ожидаемых частот. Соответственно, для этих классов получаются самые большие значения компенсации. Таким образом, мы приходим к известной истине, что равновесность в значительной степени зависит от поведения гена (фена-аллеля) в гетерозиготном состоянии.
Теперь, чтобы окончательно формализовать наш анализ, можно попытаться рассчитать приспособленность и коэффициент отбора для каждого зиготического сочетания по Райту [45]. К сожалению, рассчитать эти показатели по одному поколению в традиционном смысле нельзя, но их можно спрогнозировать при допущении, что «ожидаемое с компенсацией» отражает частоту генотипа в родительском поколении. Величину такой «провизорной» или «виртуальной» приспособленности «w’» можно выразить как отношение частоты выживших особей к ожидаемой, в нашем случае «компенсированной», чья приспособленность принимается за 1. Тогда «провизорный коэффициент отбора» s’ также будет рассчитываться из стандартной формулы s’ = 1 — w’. Для примера: в первой популяции C. annularius обнаружено 14 гетерозигот по инверсии в плече А при «компенсированной» величине — 16,6 особи. Тогда «приспособленность» будет составлять w’ = 14 : 16,6 = 0,84, а коэффициент отбора s’ = 1 – 0,84 = 0,16. Естественно, для вариантов, которые не были встречены в выборке, приспособленность принимается равной 0.
Для разовых сборов в случае высокого полиморфизма популяции можно рассчитать индекс фиксации F по Райту [32] по равнозначным формулам
F = (P – p2)(pq)–1 ≡ (2pq – H)(2pq)–1 ≡ (Q – q2)(pq)–1.
Следует помнить, что индекс фиксации отражает не тенденцию к фиксации аллеля или определенного ЗС в генофонде, а закрепление некоего состояния, характеризующегося стабильным соотношением сочетаний аллелей в целом.
В таблицах 4, 5 и 6 приведены значения «провизорной приспособленности» и индекса фиксации для всех трех изученных видов.
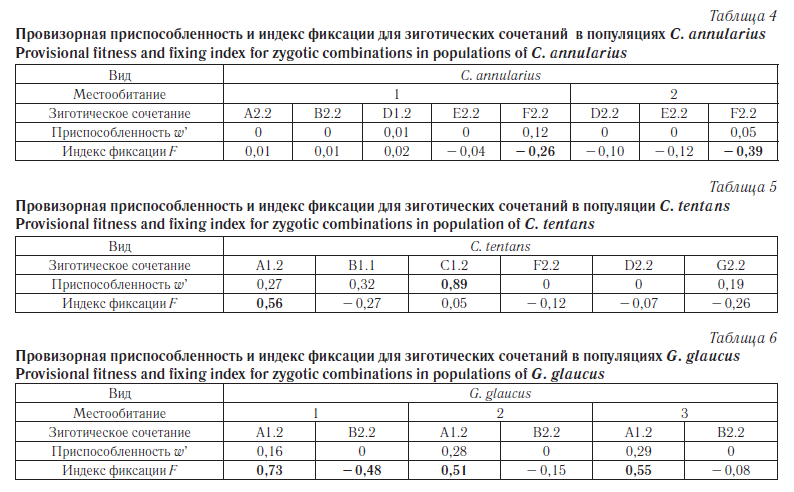
Значения приспособленности и индекса фиксации для C. annularius достаточно низки, чтобы можно было говорить об активном адаптивном поиске и перспективах стабилизации генетической структуры с каким-то определенным набором зиготических сочетаний и соответствующих им частот. Другими словами, две популяции достаточно сходны по структуре. Учитывая их географическую близость, можно предполагать активный генетический обмен в результате миграции имаго. Естественно, в таких условиях значительная дивергенция и тем более формирование хромосомных аллопатрических рас невозможно.
Значения приспособленности и индекса фиксации для C. tentans (табл. 5) позволяют сделать парадоксальное наблюдение. Несмотря на высокую приспособленность гетерозиготы С1.2, соответствующий индекс фиксации низок. Значительное преимущество гетерозигот в данном случае не означает, что популяция в какой-то момент станет полностью гетерозиготной по С1.2 в плече IIС, поскольку при панмиксии в каждом поколении потомков будут выщепляться гомозиготы. В то же время низкая приспособленность гетерозиготы A1.2 предполагает определенную тенденцию к фиксации гомозигот (0,56). И в этом случае противоречие отсутствует.
Более-менее высокой приспособленностью в популяциях G. glaucus не обладает ни одно ЗС. Однако величины индекса фиксации для плеча А значительны во всех трех популяциях. Это тот же случай, как и с C. tentans, — поддержание в популяции высокого уровня гетерозигот в плече А без окончательной фиксации. Что же касается гомозигот по инверсии в плече В, то отбор, видимо, целенаправленно отсеивает эти варианты как неадаптивные, хотя по данным табл. 3 эту тенденцию подтвердить удалось только методом «компенсации».
Как видно из таблиц 4–6, во многих случаях величина индекса фиксации близка к нулю, что свидетельствует о панмиксии в популяции. Однако у G. glaucus и C. tentans для хромосомного плеча А показатели индекса достигают значений 0,51–0,73, что может говорить о нарастании инбредности и тенденции к фиксации одного из вариантов ПДХ. Отрицательная величина (– 0,48) для плеча IВ у G. Glaucus, наоборот, может свидетельствовать об относительно высокой аутбредности. Это же явление, только в несколько меньшей степени, наблюдается в плече IIIF у C. annularius(– 0,39, – 0,26).
Еще раз следует подчеркнуть, что наши результаты получены при допущении, что наблюдаемое распределение в диаллельных локусах образуется в отсутствие взаимного влияния. То есть как независимые события. В действительности эти процессы протекает далеко не независимо. Рассмотрим распределение числа особей с разной степенью гетерозиготности в псковской популяции C. tentans. Из семи хромосомных плеч кариотипа в шести были обнаружены перестройки в гомо- и гетерозиготном состоянии. Исключив одно мономорфное плечо, составим прогноз для гексагибридного скрещивания. А ЗС объединим в классы по количеству гетерозиготных инверсий в кариотипе. Тогда теоретическое соотношение числа гетерозиготных вариантов и наблюдаемые значения частот выглядят так, как показано в таблице 7. Для удобства представления информации теоретическое соотношение генотипов пересчитаем на 40 особей, чтобы получить «нормализованные» частоты. Заметно, что в естественной популяции максимум распределения сдвинут в сторону уменьшения количества перестроек на особь. Распределение генотипов в панмиктической популяции подчиняется закономерностям бинома Ньютона. Формула Пирсона — его частный и простейший случай. То есть должно наблюдаться биномиальное распределение, которое в случае большого числа классов аппроксимируется нормальным.
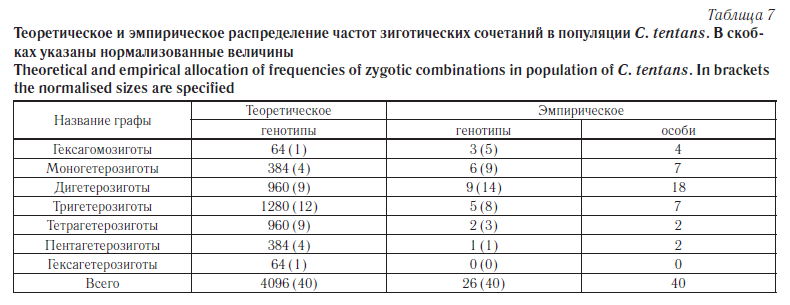
Если сравнить наблюдаемые и ожидаемые частоты генотипов, можно отметить достоверный (p > 0,05) сдвиг наблюдаемых значений в сторону минимизации числа инверсий на особь (As = 0,28; Asm = 0,37) (левосторонняя асимметрия). Можно предположить наличие движущего отбора, отсеивающего избыточно полиморфные генотипы. В то же время эксцесс отрицателен, но незначительно (Ex = – 0,14; Exm = 0,73), преимущество какого-то генотипа на выбранном уровне достоверности не проявляется.
Гораздо более отчетливо эти закономерности наблюдаются в ходе сравнения распределений ожидаемых частот генотипов и наблюдаемых частот особей — носителей соответствующих генотипов. Они различаются статистически достоверно (p > 0,05). Асимметрия реального распределения положительная (As = 0,47; Asm = 0,37), пик графика смещен в сторону минимизации числа инверсий на особь (левосторонняя асимметрия). Налицо движущий отбор, хотя в данном случае он больше заслуживает названия «препятствующего», поскольку его вектор направлен против увеличения уровня средней гетерозиготности по показателю Инверсия/Особь. Эксцесс резко положителен (Ex = 0,62; Exm = 0,73) (островершинность кривой распределения), что свидетельствует о значимом превышении в популяции численности особей с двумя гетерозиготными инверсиями по сравнению с теоретическим распределением [26]. Можно предполагать, что имеет место стабилизирующий отбор.
Это можно наглядно проиллюстрировать на графиках распределения наблюдаемых частот особей и генотипов, а также нормализованных ожидаемых частот генотипов (рис. 1). Примечательно, что два эмпирических распределения все-таки близки к биномиальному — значение хи-квадрат для эмпирического распределения генотипов и особей при одной степени свободы равно соответственно 0,29 и 3,57 (огибающие на графике), что может служить косвенным доказательством панмиксии в популяции.

На рисунке хорошо заметно смещение пиков для наблюдаемых значений, а также островершинность распределения реальных частот особей с разным числом инверсий в кариотипе. Серыми стрелками показаны предположительные направления давления естественного отбора.
ЗАКЛЮЧЕНИЕ
Пул и частоты хромосомных перестроек являются важнейшими характеристиками генетической структуры популяций, поскольку позволяют прогнозировать вектор вероятных микроэволюционных процессов. Предполагается, что инверсии (наряду с дупликациями) — самые щадящие из хромосомных аберраций, которые в наименьшей степени влияют на жизнеспособность особей, в то время как остальные зачастую летальны или сублетальны. Значение гетерозигот по инверсиям в свое время подчеркивал Ф. Добржанский [37], обнаруживший в определенных условиях их повышенную жизнеспособность благодаря гетерозису. Достоверно доказана зависимость частоты инверсий от условий обитания. В середине прошлого века для Drosophila была открыта клинальная изменчивость популяций согласно географическому градиенту, установлено влияние высоты над уровнем моря, а также сезона [38]. Для личинок хирономид удалось установить биометрический эффект инверсий [42]. Можно привести в пример ставшие классическими работы, в которых доказано существование «городской» и «сельской» хромосомных рас у дрозофилы, различающихся по частотам инверсий в кариофонде [12]. В этих расах, несмотря на принудительную взаимную интродукцию, частоты инверсий неизменно возвращались на прежний уровень, свойственный расе [6]. У родственных хирономидам мошек (Simuliidae) полиморфизм по инверсиям считается бесспорной адаптивной стратегией [33]. У видов комаров из рода Anopheles обнаружено статистически значимое изменение частот определенных перестроек в условиях совместного культивирования на преимагинальных стадиях [11]. Межвидовая конкуренция в культуре является важным фактором отбора, несмотря на то что конкуренции за ресурсы быть не должно, поскольку они в избытке. Подобных примеров существует достаточно много. Все они говорят о том, что частоты «квазинейтральных» перестроек напрямую связаны с адаптивными возможностями видов и популяций, их составляющих. А уровень полиморфизма, как правило, может служить надежным показателем потенциала приспособленности. Однако убедительных моделей механизмов влияния инверсий на жизнеспособность у двукрылых до настоящего времени нет. Теория «коадаптированных комплексов» Добржанского [38] и предполагаемое действие эффекта положения по Стегнию [29] применительно к двукрылым пока что остаются теориями.
Единицей организации и хранения знания в математической биологии является математическая модель, построенная для изучения хотя бы одной целостной характеристики биосистемы [7]. При анализе моногибридного скрещивания в природных популяциях для разовых выборок совокупность таких показателей, как оценка ожидаемых частот, «компенсированных» частот, их отклонение от реальных значений, «провизорная» приспособленность (и коэффициент отбора), а также индекс фиксации, — достаточные составные части модели, позволяющей описать единичную целостную характеристику — «состояние одного хромосомного плеча в условиях панмиксии под давлением отбора».
В реальных условиях кариофонды высокополиморфных видов хирономид нередко насчитывают десятки типов наследуемых перестроек, большую часть которых составляют так называемые квазинормальные инверсии, поскольку их эффект для жизнеспособности особей и приспособленности популяций неясен. В зависимости от региона и условий обитания набор инверсий в кариофонде популяций значительно варьирует. Однако обычно в природных популяциях уровень гетерозиготности в среднем не превышает значения N/особь, где N — число хромосомных плеч в кариотипе. У хирономид это число, как правило, меньше семи. Явление «рассредоточения» гетерозиготных инверсий по разным хромосомам известно довольно давно [36]. При условии, что в каждом из хромосомных плеч имеется не более одной инверсии, синапсис взаимоинвертированных гомологов в гаметогенезе должен блокировать кроссинговер и протекать без значительных потерь генетической информации. Такое явление нередко наблюдается в природных популяциях того же C. tentans, когда буквально каждое плечо, включая малую хромосому кариотипа, несет перестройку в гетерозиготном состоянии [13].
Среди исследователей политенных хромосом математически серьезно проблему неравновесности поднимали Martin и Wulker [43], отметившие ее удивительную стабильность и также связавшие уникальность генетической структуры исследованных популяций с условиями обитания популяций. Таких работ по хирономидам, к сожалению, немного. В нашей работе сделана попытка проанализировать возможные направление и силу воздействия только одного микроэволюционного фактора на основе единичных сборов. Тем не менее удалось оценить не только приблизительную приспособленность разных ЗС, но и сделать достаточно правдоподобное заключение о направлении и характере отбора. Безусловно, в природных популяциях имеют место и остальные микроэволюционные явления. Мы остановимся только на некоторых фактах, полученных при исследовании популяций тех же хирономид. Миграции и параллельное нарушение жизненного цикла может приводить к межвидовой гибридизации, как это наблюдается, например, между C. plumosus и C. nuditarsis [40], а также между C. riparius и C. piger [25]. Мутационный процесс, миграция и дрейф генов могут формировать уникальную структуру популяций в результате действия эффекта «бутылочного горла», когда все особи несут сочетание двух разных инверсионных ПДХ (A2A3), но при этом не обнаруживаются гомозиготы по этим последовательностям (A2A2) и (A3A3) [4]. Описаны факты, когда в популяциях хирономид хромосомные инверсии присутствовали только в гетерозиготном состоянии [1, 27, 44]. Эти случаи можно охарактеризовать как достижение предельной степени неравновесности с индексом фиксации F = 1. Мономорфные по перестройкам виды также предельно неравновесны, все ПДХ в их генофонде обладают максимальной приспособленностью (w = 1), а индекс фиксации максимален (F = 1), что означает временный микроэволюционный тупик.
Совсем недавно была установлена определенная зависимость наследования разных перестроек, когда зиготические сочетания образуются неслучайно, то есть имеет место частичная сцепленность [2]. И это еще одна из многих причин несоблюдения закона Харди – Вайнберга. Связи и взаимозависимости адаптационных и эволюционных механизмов — в большинстве своем хорошо изученные и строго смоделированные — в природных условиях остаются непредсказуемыми. Для изучения по отдельности прочих микроэволюционных факторов, действующих в природных популяциях, требуются уникальные для каждого случая методы. Результаты их применения впоследствии необходимо синтезировать для получения целостной картины. Но есть опасение, что множество допущений и условностей еще на этапах планирования и моделирования приведет к результату, далекому от реального состояния популяций в природных условиях.
Анализируя роль неравновесности в наиболее широком смысле, следует вспомнить теорию управления применительно к биологическим системам. Концепция самосохранения живых систем обусловлена способностью поддерживать стационарное неравновесное состояние [23]. Фундаментальная теорема естественного отбора Фишера [39] постулирует возрастание приспособленности популяции под действием отбора независимо от начальных условий. Естественный отбор — единственный фактор, увеличивающий среднюю приспособленность популяции. По Фишеру, приспособленность популяции должна возрастать даже в условиях стабильной и длительной неравновесности, благодаря которой поддерживается генетический гомеостаз.
Подводя итог, можно предложить ряд выводов.
1. Популяционный анализ трех видов хирономид, сделанный на основе разовых сборов, позволил установить ряд закономерностей. Популяции C. annularius неравновесны по перестройкам в плече F хромосомы III. Популяции C. tentans и G. glaucus неравновесны по перестройкам в плече A хромосомы I. Генетическая структура популяции C. tentans могла сформироваться в результате естественного отбора, действие которого направлено против особей с высоким уровнем гетерозиготности.
2. Микроэволюционные тенденции вполне можно оценивать на основе «скрининга», разового сбора, временног&
About the authors
Sergey V. Zhirov
Zoological Institute
Author for correspondence.
Email: svzhiroff@mail.ru
отделение кариосистематики Russian Federation
Sergey V. Mylnikov
St Petersburg State University
Email: S.mylnikov@spbu.ru
school of biology, Department of Genetics and Biotechnology Russian Federation
References
- Белянина С.И. Сравнительная кариотипическая характеристика Chironomus annularius (Diptera, Chironomidae) из различных географических зон // Зоологический журнал. — 1981. — Т. 60. — Вып. 7. — С. 1030–1039. [Belyanina SI. Relative karyotypical characteristic of Chironomus annularius (Diptera, Chironomidae) from various geographical regions. Zoological Journal. 1981;60(7):1030-1039. (In Russ.)]
- Белянина С.И. Хромосомные и геномные мутации у Chironomus plumosus (L.) (Diptera, Chironomidae) из Новозыбковского района Брянской области // Генетика. — 2012. — Т. 48. — № 4. — С. 495–502. [Belyanina SI. Chromosomal and genomic mutations at Chironomus plumosus (L.) (Diptera, Chironomidae) from Novozybkovsky area of the Bryansk region // Genetics. 2012;48(4):495-502. (In Russ.)]
- Белянина С.И., Дурнова Н.А. Морфология и хромосомы фитофильного Glyptotendipes glaucus (Diptera, Chironomidae) из водоемов Саратовской области. 2. Кариотипический анализ // Зоологический журнал. — 1998. — Т. 77. — № 2. — С. 243–251. [Belyanina SI, Durnova NA. Morphology and chromosomes of phytophilous Glyptotendipes glaucus (Diptera, Chironomidae) from reservoirs of the Saratov region. 2. The Karyotipical analysis. Zoological Journal. 1998;77(2):243-251. (In Russ.)]
- Белянина С.И., Сигарева Л.Е., Логинова Н.В. Новый вид Chironomus curabilis sp. n. (Diptera, Chironomidae) // Зоологический журнал. — 1990. — Т. 69. — Вып. 5. — С. 60–70. [Belyanina SI, Sigareva LE, Loginova NV. New species Chironomus curabilis sp. n. (Diptera, Chironomidae). Zoological Journal. 1990;69(5):60-70. (In Russ.)]
- Беркинблит М.Б. Генетические основы эволюции: методические разработки для учащихся биологического отделения ВЗМШ АПН СССР при МГУ им. М. В. Ломоносова. — М., 1987. — 44 с. [Berkinblit MB. Genetical bases of evolution: methodical recommendations for students of biological branch VZMS NPA of the USSR at the Moscow State University of M.V. Lomonosov. Moscow; 1987. 44 p. (In Russ.)]
- Борисов А.И. Взаимодействие хромосом Drosophila funebris городских и сельских рас в экспериментальных популяциях // Генетика. — 1970. — Т. 6. — № 2. — С. 81–89. [Borisov AI. Interaction of chromosomes at city and rural strains of Drosophila funebris in experimental populations. Genetics. 1970;6(2):81-89. (In Russ.)]
- Брусиловский П.М. Становление математической биологии. — М.: Знание, 1985. — 63 с. [Brusilovsky PM. Formation of mathematical biology. Moscow; 1985. 63 p. (In Russ.)]
- Ван дер Варден Б.Л. Математическая статистика. — М., 1960. — 434 с. [Van der Varden BL. Mathematical statistics. Moscow; 1960. (In Russ.)]
- Гланц С. Медико-биологическая статистика. — М.: Практика, 1999. — 459 с. [Glants S. Medical and biologic statistics. Moscow; 1999. 459 p. (In Russ.)]
- Глотов Н.В., Животовский Л.А., Хованов Н.В., и др. — Л.: ЛГУ, 1982. — 264 с. [Glotov NV, Zhivotovskiy LA, Khovanov NV, et al. Leningrad; 1982. 264 p. (In Russ.)]
- Гордеев МИ. Адаптивные стратегии в популяциях малярийных комаров: автореф. дис. … д-ра биол. наук. — Томск, 1997. — 42 с. [Gordeev MI. Adaptable strategy in populations of malarial mosquitoes. [dissertation]. Tomsk; 1997. (In Russ.)]
- Дубинин Н.П., Тиняков Г.Г. Инверсии на границах экологических рас у Drosophila funebris // ДАН СССР. — 1947. — Т. 55. — № 79. — С. 643–651. [Dubinin NP, Tinjakov GG. Inversions on borders of ecological races at Drosophila funebris. DAN USSR. 1947;55(79):643-651. (In Russ.)]
- Жиров С.В. Хромосомный и геномный полиморфизм в популяциях хирономид Псковской области: aвтореф. дис. … канд. биол. наук. — Л., 1994. 16 с. [Zhirov SV. Chromosomal and genomic polymorphism in chironomid populations at the Pskov area. [dissertation] Leningrad; 1994. (In Russ.)]
- Ивантер Э.В., Коросов А.В. Основы биометрии. — Петрозаводск: ПГУ, 1992. — 164 с. [Ivanter EV, Korosov AV. Biometry bases. Petrozavodsk; 1992. 164 p. (In Russ.)]
- Кайданов Л.З. Генетика популяций. — М.: Высшая школа, 1996. — 320 с. [Kajdanov LZ. Genetics of populations. Moscow; 1996. 320 p. (In Russ.)]
- Кикнадзе И.И., Айманова К.Г., Гундерина Л.И., и др. Хромосомный полиморфизм в уральских и сибирских популяциях Camptochironomus tentans // Зоол. журн. — 1993. — Т. 72. — С. 59–75. [Kiknadze II, Ajmanova KG, Gunderina LI, et al. Chromosomal polymorphism in the Ural and Siberian populations of Camptochironomus tentans. Zoological Journal. 1993;72:59-75. (In Russ.)]
- Кикнадзе И.И. Популяционная изменчивость. Кариотипы и хромосомный полиморфизм сибирских видов хирономид (Diptera, Chironomidae) // Сибирский экологический журнал. — 2000. — № 4. — С. 445–460. [Kiknadze II. Population variability. Karyotipes and chromosomal polymorphism of the Siberian species of chironomids (Diptera, Chironomidae). The Siberian ecological journal. 2000;4:445-460. (In Russ.)]
- Кикнадзе И.И., Голыгина В.В., Истомина А.Г., Гундерина Л.И. Закономерности хромосомного полиморфизма при дивергенции популяций и видов у хирономид (Diptera, Chironomidae) // Сибирский экологический журнал. — 2004. — Т. 11. — № 5. — С. 635–651. [Kiknadze II, Golygina VV, Istomina AG, Gunderina LI. Laws of chromosomal polymorphism and diversity of the populations and species of chironomids (Diptera, Chironomidae). The Siberian ecological journal. 2004;11(5):635-651. (In Russ.)]
- Лакин Г.Ф. Биометрия. — М.: Высшая школа, 1990. — 352 с. [Lakin GF. Biometry. Мoscow; 1990. 352 p. (In Russ.)]
- Ли Ч. Введение в популяционную генетику. — М.: Мир, 1978. — 555 с. [Li Ch. Introduction in population genetics. Мoscow; 1978. 555 p. (In Russ.)]
- Меттлер Л., Грегг Т. Генетика популяций и эволюция. — М.: Мир, 1972. — 324 с. [Mettler L, Gregg T. Genetics of populations and evolution. Moscow; 1972. 324 p. (In Russ.)]
- Морозов Е.И., Тарасевич Е.И., Анохина В.С. Генетика в вопросах и ответах. — Минск: Университетское, 1989. — 288 с. [Morozov ЕI, Tarasevich ЕI, Anokhina VS. Genetics in questions and answers. Minsk; 1989. 288 p. (In Russ.)]
- Новосельцев В.Н. Теория управления и биосистемы. — М.: Наука, 1978. — 320 с. [Novoseltsev VN. The control and biosystem theory. Moscow; 1978. 320 p. (In Russ.)]
- Петрова Н.А., Жиров С.В. Цитогенетическое сравнение популяций комара-звонца Glyptotendipes glaucus (Meigen, 1818) (Diptera, Chironomidae) Северо-Запада России и Украины (зона Чернобыля) // Экологическая генетика. — 2012. — Т. 9. — № 2. — С. 9–16. [Petrova NA, Zhirov SV. Cytogenetical comparison of populations of midge Glyptotendipes glaucus (Meigen, 1818) (Diptera, Chironomidae) the Northwest of Russia and Ukraine (a region of Chernobyl). Ecological genetics. 2012;9(2):9-16. (In Russ.)]
- Петрова Н.А., Жиров С.В., Арутюнова К.В., Арутюнова М.В. О возможности спонтанной межвидовой гибридизации в природе представителей сиблинг-видов Chironomus riparius Kiefferи Chironomus piger Strenzke из Армении (Diptera, Chironomidae) // Цитология. — 2014. — Т. 56. — № 2. — С. 170–74. [Petrova NA, Zhirov SV, Harutjunova KV, Harutyunova MV. About possibility of spontaneous interspecific hybridization in the nature of representatives of sibling-species Chironomus riparius Kieffer and Chironomus piger Strenzke from Armenia (Diptera, Chironomidae). Cytology.2014;56(2):170-174. (In Russ.)]
- Плохинский Н. А. Биометрия. — М.: МГУ, 1970. — 367 с. [Plokhinsky NA. Biometrija. Moscow; 1970. 367 p. (In Russ.)]
- Полуконова Н.В. Новые последовательности дисков хромосом в кариофонде Chironomus curabilis Beljanina, Sigareva, Loginova (Diptera, Chironomidae) // Кариосистематика беспозвоночных животных III. — М., 1996. — С. 62–64. [Polukonova NV. New chromosome disk sequences in the karyofund of Chironomus curabilis Beljanina, Sigareva, Loginova (Diptera, Chironomidae). In: Karyosystematics of invertebrate animals III. Moscow; 1996:62-64. (In Russ.)]
- Рокицкий П.Ф. Биологическая статистика. — Минск: Вышэйшая школа, 1973. — 320 с. [Rokitsky PF. The biological statistics. Minsk; 1973. 320 p. (In Russ.)]
- Стегний В.Н. Популяционная генетика малярийных комаров. — Томск: Изд-во ТГУ, 1991. — 136 c. [Stegnyj VN. Population genetics of malarial mosquitoes. Tomsk; 1991. 136 p. (In Russ.)]
- Фогель Ф., Мотульски А. Генетика человека. В 3 т. — М.: Мир, 1990. — T. 3. — 366 с. [Fogel F, Motulski A. Human genetics. In 3 vol. Moscow; 1990. Vol. 3. 366 p. (In Russ.)]
- Хедрик Ф. Популяционная генетика. — М.: Техносфера, 2003. — 592 с. [Hedrick F. Population genetics. Moscow; 2003. 592 p. (In Russ.)]
- Хромов-Борисов Н.Н. Биометрические аспекты популяционной генетики // Кайданов Л.З. Генетика популяций. — М.: Высш. шк., 1991. — 320 с. [Khromov-Borisov NN. Biometrical aspects of population genetics. In: Kajdanov L.Z. Genetics of populations. Moscow; 1991. 320 p. (In Russ.)]
- Чубарева Л.А. Политенные хромосомы кровососущих мошек (Simuliidae, Diptera) и их использование в систематике: Автореф. дис. … д-ра биол. наук. — Л., 1986. — 48 с. [Chubareva LA. Polytene chromosomes of blood-sucking flies (Simuliidae, Diptera) and their use in systematics. [dissertation] Leningrad; 1986. 48 p. (In Russ.)]
- Чубарева Л. А., Петрова Н.А. Цитогенетический метод анализа хромосом у хирономид: Методическое пособие по изучению хирономид. — Душанбе: Дониш, 1982. — С. 64–73. [Chubareva LA, Petrova NA. A cytogenetical method of the analysis of chromosomes of the chironomids. The methodical recommendations on studying of the chironomids. Dushanbe; 1982. P. 64-73. (In Russ.)]
- Шифман В. Н. Исследование полиморфизма в детерминированной модели двухлокусной панмиктической популяции // Исследования по теоретической генетике. — Новосибирск, 1972. — С. 138–152. [Shifman VN. Polymorphism research in the determined model of two-loci panmictic populations. In: Researches on theoretical genetics. Novosibirsk; 1972. P. 138-152. (In Russ.)]
- Щербаков Е.С. О разнохромосомном размещении гетерозиготных инверсий как механизме повышения адаптации популяций // Генетика. — 1968. — Т. 4. — № 6. — С. 182–184. [Scherbakov ES. About allochromosomal placement of heterozygous inversions as the mechanism of increase of acclimatisation of populations. Genetics. 1968;4(6):182–184. (In Russ.)]
- Dobzhansky Th. Genetics and the origin of species. N.Y. and London: Columbia Uneversity Press; 1964.
- Dobzhansky Th. Genetics of Evolutionary Process. N.Y. and London: Columbia Univ. Press; 1970.
- Fisher RA. The General Theory of Natural Selection. N.Y.: Dower Publ.; 1958.
- Fisher J, Rosin S. Bastarde zwischen Chironomus plumosus L. und Chironomus nuditarsis Str. Arch. Julius Klaus-Stift. 1967;42:30-42.
- Kiknadze II, Istomina AG, Golygina VV. The karyotype and chromosome polymorphism of the Holarctic species Chironomus “annularius” sensu Strenzke, 1959 (Diptera, Chironomidae). Euroasian Entomological Journal. 2012:11(2):95-114.
- Martin J. Biometrical effect of the inversions polymorphism of Kiefferulus intertinctus (Skuse). Aust J Biol Sci. 1973;26:1371-1377.
- Martin J, Wulker W. Inversion polymorphism in Chironomus staegeri Lundbeck. Canadian Journal of Genetics and Cytology, 1971;13:306-321.
- Michailova P, Jablonska-Brana I. Chromosome polymorphism of Camptochironomus tentans (Fabricius 1805) (Diptera, Chironomidae) from Luknajno (Mazurian Lakeland), Poland. Acta Zoologica Bulgarica. 2008;60(2):155-163.
- Wright S. Evolution: Selected Papers. In: Sewall Wright and Evolutionary Biology. Ed by W. B. Provine. Chicago, London: University of Chicago Press; 1986.
Supplementary files











